本当にできてる？標準偏差から予測する将来リターンの計算方法

投資信託を購入する前に1年後のリターンがどの程度になるのか、誰しもが予測する方法はないかと思っています。

もちろん将来のことなので、わからないと言えば、それまでなのですが、ある計算をすることで、1年後のリターンを統計的に予測することができます。

ある程度、投資信託について勉強している人であれば、何となくはご存じかと思いますが、思った以上にちゃんと理解していない人が多いことに気づきました。

ですので、今日はリスクについて、事細かくお話ししたいと思います。

リスクと標準偏差の関係性

株式や債券などの投資信託の基準価格は、常に上昇・下落を繰り返しながら推移しています。

また、一般的には株式よりも債券の方が上昇・下落の変動幅が小さいなど、資産クラス間には基準価格の変動幅の違いが見られます。

運用の世界では、こうした価格変動性をリスクと呼びます。

私たちの日常の生活では、リスクとは「危険」という意味で使われますが、運用では「運用の失敗、損失」ではなく「リターン予測の不確実性、期待したリターンに対する実際のリターンのバラつき・変動幅」という意味で用いられます。

そして、このリスクの変動幅を統計的に数値化したものが「標準偏差（σ：シグマ）」です。

一般に、投資信託など運用の世界で「リスクが大きい・小さい」と言う場合、この標準偏差の大小を指しています。

よくリスクが高い＝下落する幅が大きいと思われがちですが、その一方で、上昇する幅も大きいということを忘れてはいけません。

標準偏差の注意点

標準偏差については、言葉も難しく、複雑な数式が絡んでくるため、あまりしっかりと理解しようと思ったことがないかもしれません。

しかし、理解が間違っていると後から痛い目を見る可能性がありますので、これを機会にしっかり理解しておきましょう。

標準偏差は「平均リターン」に対する「実際のリターン」の変動幅を示します。

つまり実際のリターンがどの程度の確率で標準偏差の範囲内に収まるかを推定することができるのです。

下図を見ると、少しイメージが湧くかもしれませんが、平均＝平均リターンとお考え下さい。

そして、1σが1年間の平均標準偏差（基準価額の変動幅）です。

そうすると、±1σの範囲で年間リターンが収まる確率は65%、±2σの範囲でリターンが収まる確率が95%と推定できるわけです。

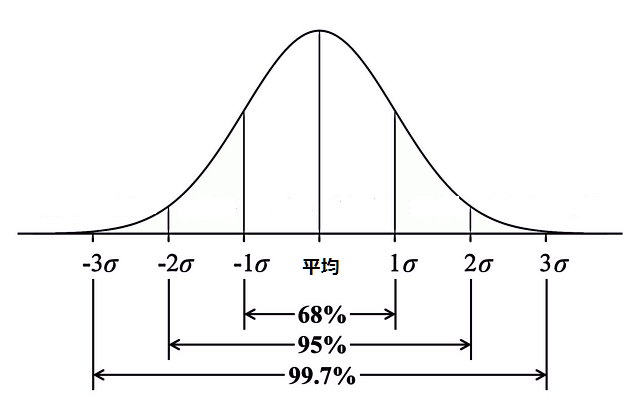
よく±1σでリターンの変動幅を推定している方がいますが、±1σでは、その範囲内に収まる可能性は65%ということになりますので、あまり信頼できる数値とは言えません。

ですので、1年後のリターン範囲を高い確度で予測したいのであれば、±2σで計算する必要があります。

また、標準偏差は平均リターンからの変動幅です。標準偏差だけみて、±2σを計算し、リターンは±2σの範囲に収まるんだと勘違いする人も多いのでこれも注意が必要です。

具体例があったほうがわかりやすいと思いますので、ひふみプラスの事例をもとに、計算してみましょう。

実際のリスクの計算方法

こちらはひふみプラスのトータルリターンおよび標準偏差をまとめたものです。

このデータ自体はモーニングスターですが、SBI証券やYAHOOファイナンス等でも確認できます。

では、具体的に1年後のリターンの範囲を計算してみましょう。

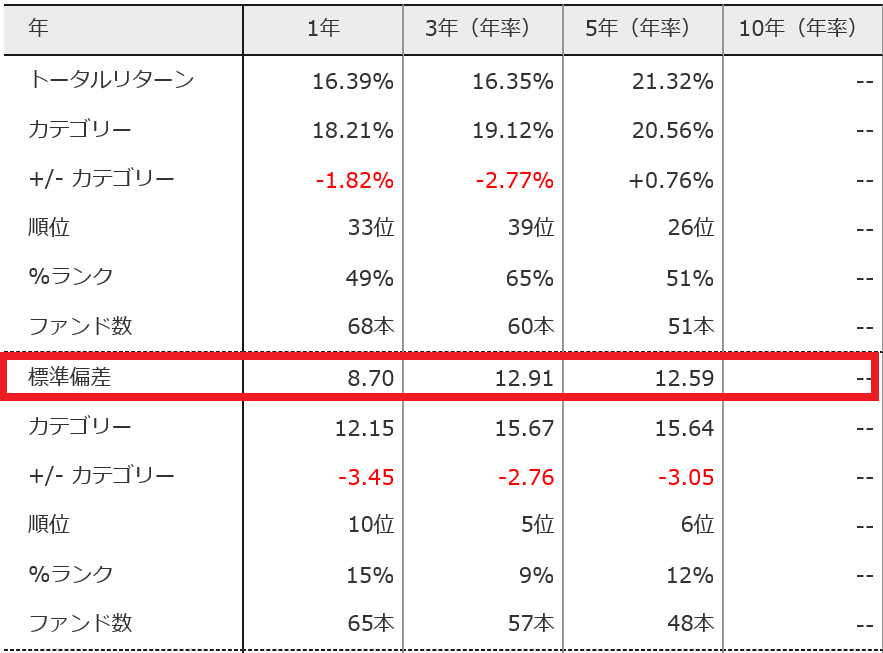
まず、問題となってくるのは、1年平均か、3年平均か、5年平均かどの数字を使うのかという点です。

一見すると、1年平均のリターンと標準偏差から計算するように思う人もいるのではないでしょうか。

しかし、ここでは、できるだけ長い期間の平均を使うのが正解です。

イメージしてもらえばわかりますが、1年間の平均リターンは、その年の市場環境の影響を強く受けますので、良いときもあれば、悪いときもあります。

そうすると、当然、平均リターンや標準偏差もその年その年で大きく変動してしまいます。

そこで、5年平均を使うと、1年ごとの市場環境の影響をできるだけ平準化できるので、今後の基準価額の変動幅を予測するうえでは、精度が高くなるというわけです。

ですので、今回の場合は、平均リターンが21.32%、標準偏差σは12.59%を使います。

これをもとに計算すると、1年後のリターンの範囲は65%の確率で21.32%±12.59%の範囲に収まり、95%の確率で21.32%±25.18%の範囲に収まると予測できるわけですね。

さきほども言いましたが、標準偏差だけをみて、今後1年間のリターンは±25.18%以内に収まると考えないように注意をしてください。

あくまでも平均リターン（ここでは、21.32%）を基準に計算します。

これで計算のイメージはつかめたと思います。

標準偏差の利用方法

さて、標準偏差を用いて、将来リターンを予測する方法は理解できたと思います。

標準偏差は単純にリターンの範囲を予測することにも使えますが、もう一つ別の使い方もすることができます。

それは、アセットクラスごとの標準偏差の比較です。

例えば、日経225に連動するインデックスファンドや先進国株式のインデックスファンドであれば、標準偏差は14～16程度です。

J-REITの場合は約半分の7～8程度、グローバルREITの場合は、13～15程度です。

だいたいの数字を覚えておくことで、たとえば、バランス型ファンドへの投資を検討しており、標準偏差が14～15程度だったとすると、実は株式ファンドと同じ程度のリスクを取っていることがわかります。

まとめ

いかがでしたでしょうか？

残念ながら、統計的な方法ではリーマンショックのような大暴落が起きたときに、それを事前に予測できるような計算方法ではありません。

しかし、統計的に算出した数値でしかないと言われれば、それまでですが根拠とする数字が何もないよりは判断に役立つのではないでしょうか。

名前が難しいので、毛嫌いしてしまう人も多いですが、一度使い方を覚えてしまえば、難しい計算をするわけでもありませんので、案外役立ちますよ。